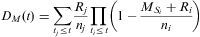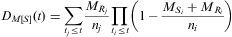Analizar el tiempo de supervivencia libre de enfermedad y la supervivencia relativa en mujeres diagnosticadas de cáncer de mama en la provincia de Gipuzkoa en un contexto de riesgos competitivos, valorando las diferencias encontradas entre el uso directo del estimador de Kaplan-Meier y el método de decrementos múltiples por un lado y la supervivencia relativa por otro.
MétodosSe consideraron todos los casos de cáncer de mama registrados en la provincia de Gipuzkoa durante los años 1995 y 1996 en estadio distinto del IV, y se hizo un seguimiento de 8 años para la recidiva y de 10 años para la supervivencia. Se analizó el tiempo de supervivencia libre de enfermedad mediante el método de decrementos múltiples. Asimismo, también se analizó el tiempo de supervivencia observado y corregido por la mortalidad esperada de la población, conocido como supervivencia relativa.
ResultadosLa estimación de la probabilidad de recidiva a los 8 años por el método de decrementos múltiples es un 8,8% inferior a la obtenida por el método de Kaplan-Meier. La diferencia entre la supervivencia observada y la relativa a los 10 años es del 10,8%. Ambos resultados indican que, en este caso, el método de Kaplan-Meier sobrestima tanto la probabilidad de recaída como la de muerte por la enfermedad.
ConclusionesDos cuestiones que muchas veces se obvian al realizar un análisis de supervivencia son, por un lado, que la no independencia entre el tiempo de supervivencia y el tiempo de censura hacen no interpretables los resultados obtenidos por el estimador de Kaplan-Meier, y por otro el hecho, hasta hora incuestionable, de que de una manera u otra todos causamos fallo y, desde este planteamiento, en el estudio del tiempo de supervivencia hay que tener presente la probabilidad de fallo en la población general de referencia. En los resultados obtenidos se observa que utilizar de manera superficial el estimador de Kaplan-Meier comporta una sobrestimación tanto de la probabilidad de recidiva como de la mortalidad debida a la enfermedad.
To analyze time of disease-free survival and relative survival in women diagnosed with breast cancer in the province of Gipuzkoa within the context of competing risks by assessing differences between the direct use of the Kaplan-Meier estimator and the multiple decrement method on the one hand, and relative survival on the other.
MethodsAll registered breast cancer cases in Gipuzkoa in 1995 and 1996 with stages other than stage IV were included. An 8-year follow-up for recurrence and a 10-year follow-up for survival were performed. Time of disease-free survival was studied by the multiple decrement model. Observed survival and survival corrected by the expected mortality in the population (relative survival) were also studied.
ResultsEstimation of the probability of recurrence at 8 years with the multiple decrement method was 8.8% lower than that obtained with the Kaplan-Meier method. The difference between the observed and relative survival rates at 10 years was 10.8%. Both results show how, in this case, the Kaplan-Meier estimator overestimates both the probability of recurrence and that of mortality from the disease.
ConclusionsTwo issues are often overlooked when performing survival analyses: firstly, because of the lack of independence between survival time and censoring time, the results obtained by the Kaplan-Meier estimator are uninterpretable; secondly, it is an incontrovertible fact that one way or another, everyone causes failures. In this approach, survival analyses must take into account the probability of failure in the general population of reference. The results obtained in this study show that superficial use of the Kaplan Meier estimator overestimates both the probability of recurrence and that of mortality caused by the disease.
Cuando se realiza un estudio sobre el tiempo necesario para que suceda un evento, uno de los problemas habituales es que el tiempo necesario para que el suceso en estudio se produzca entre en competencia con otros eventos que lo imposibilitan (en el estudio de la supervivencia libre de enfermedad, que la persona fallezca por otras causas antes de que se produzca una recaída). Este tipo de censuras no satisfacen las hipótesis exigidas para que los estimadores usuales para las curvas de supervivencia funcionen adecuadamente (el estimador de Kaplan-Meier1 asume que el tiempo hasta la recaída de una persona fallecida antes de que ésta se produzca [por tanto censurada] será superior al tiempo de vida observado), y por ese motivo es recomendable usar métodos que tengan en cuenta tales particularidades, como por ejemplo el método de los decrementos múltiples2, que teniendo en cuenta la existencia de censuras informativas (mujeres que fallecen antes de la recaída) obtiene resultados sobre el riesgo real de recaída. Por otro lado, en el estudio del tiempo de supervivencia de las personas que sufren una determinada enfermedad, una de las cuestiones que con demasiada frecuencia se obvian es el hecho de que, con independencia de que se tenga una enfermedad o no, hay una mortalidad de base que afecta a toda la población. Así las cosas, para tener una idea más real de los efectos sobre el tiempo de supervivencia de la enfermedad en estudio no suele ser suficiente con estudiar la supervivencia observada y calcular el clásico estimador de Kaplan-Meier. En este contexto surge el análisis de supervivencia relativa3, basado en corregir la supervivencia observada o cruda por la supervivencia esperada en la población general de referencia, la cual debe tener en cuenta los posibles efectos sobre la supervivencia de determinadas covariables presentes en la muestra4 (clase socioeconómica, sexo, etc.).
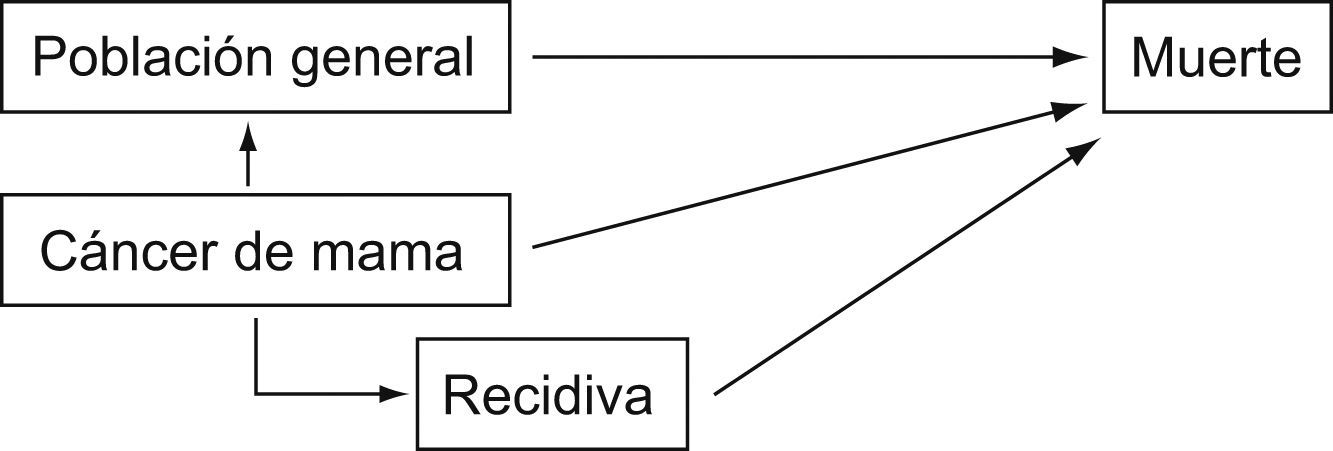
El objetivo principal de este trabajo es ilustrar las grandes diferencias que se pueden presentar al no considerar estas circunstancias. Para ello, por un lado se analiza la supervivencia libre de enfermedad (como sucesos secundarios también se estudian la supervivencia global y la supervivencia después de la recaída) en mujeres diagnosticadas de cáncer de mama no metastásico durante los años 1995 y 1996 en la provincia de Gipuzkoa, siguiendo un esquema similar al usado por Llorca et al5, en el cual se incorpora el método de los decrementos múltiples para estudiar los sucesos principal (recaída) y secundario (muerte). Por otro lado, para estudiar el efecto de la enfermedad sobre la supervivencia se tiene en cuenta la mortalidad de la población de referencia y se utiliza el método de supervivencia relativa.
MétodosSe incluyeron todas las mujeres residentes en Gipuzkoa, diagnosticadas de cáncer de mama invasivo (636) en los años 1995 y 1996. Los casos se identificaron en el Registro de Cáncer Poblacional de Gipuzkoa. Se excluyeron aquellos casos cuya única fuente de identificación era el boletín estadístico de defunción (14; 2,2%), aquellos con extensión diseminada en el momento del diagnóstico (61; 9,6%) y aquellos de los cuales se desconocía si se había producido una recaída (56; 8,8%).
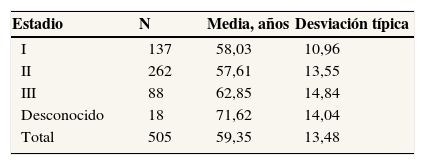
Las características de la paciente y del tumor en el momento del diagnóstico, y la existencia de recidiva, se recogieron de los registros de tumores hospitalarios o, en su defecto, de la revisión de las historias clínicas tanto hospitalarias como de atención primaria. El tiempo de seguimiento para determinar la aparición de recidiva fue hasta diciembre de 2004, lo que supone un seguimiento de 8 años para este suceso. Con el Índice Nacional de Defunciones se registraron las muertes por todas las causas ocurridas hasta diciembre de 2007, lo que permite prolongar el seguimiento de la supervivencia hasta los 10 años. Se consideraron, por tanto, 505 casos (79,4%), y se registraron 145 (28,7%) recidivas y 43 (8,5%) muertes antes de producirse una recidiva. En la tabla 1 se muestran algunos estadísticos descriptivos sobre las características de la muestra. En una publicación anterior6 se encuentra más información sobre la población incluida en este estudio.
Se estudiaron el tiempo hasta la recidiva (supervivencia libre de enfermedad) y el tiempo de supervivencia observada y relativa; el cociente entre la supervivencia observada y la supervivencia esperada de la población de referencia teniendo en cuenta los distintos riesgos existentes en la población general; fallecer por otra causa antes de producirse la recaída en el primer caso; y el riesgo asociado a estar vivo en el segundo.
Para la consistencia del estimador de Kaplan-Meier se requiere que el tiempo de supervivencia y el de censura sean independientes, y que las censuras sean no informativas. En el estudio de la supervivencia libre de enfermedad se sabe que, a mayor tiempo sin recaída, mayor probabilidad de muerte por otras causas, y por tanto mayor probabilidad de censura. Además, este tipo de censura es excluyente, ya que elimina la posibilidad del evento en estudio y por ello no debe considerarse como una censura no informativa. El método de decrementos múltiples, suponiendo nula la probabilidad de que la recaída y la muerte se produzcan simultáneamente, consiste en calcular el estimador de Kaplan-Meier (éste puede interpretarse como la probabilidad de que un individuo adquiera el estado en estudio antes de un determinado momento t) para el suceso doble: muerte (M) o rediviva (R), para después corregirlo en función de que el suceso que se ha producido sea el considerado como principal (R) o como secundario (M). La expresión analítica del estimador del riesgo del evento, si MS denota la muerte antes de producirse la recidiva, viene dada por:
donde Rj y nj denotan, respectivamente, el número de individuos con recidiva y sometidos a riesgo justo antes del instante tj, y MSi, Ri, y ni el número de individuos fallecidos antes de producirse la recidiva, el número de individuos con recidiva y el número de individuos sometidos a riesgo justo antes del instante ti, respectivamente.Este método se amplía al estudio de un suceso secundario: calcular la probabilidad de muerte después de sufrir una recidiva, estimando el riesgo de que se produzca este evento de una manera similar a la anterior. Por un lado se calculó la probabilidad del suceso doble (muerte antes de la recidiva y muerte después de la recidiva) mediante el estimador de Kaplan-Meier, para luego corregirlo por la probabilidad del suceso de interés (muerte tras la recidiva), resultando el estimador:
donde MRi es el número de mujeres que mueren tras la recidiva justo antes del instante ti.Para estimar la supervivencia general, tanto desde el momento del diagnóstico (toda la población) como desde el momento de la recaída (únicamente mujeres con recidiva), se tuvo en cuenta la mortalidad general para los periodos 1995–1999 y 2000–2005, agrupada por edades de año en año (una tasa para cada año de edad), de la población en estudio (Instituto Vasco de Estadística, www.eustat.es), usando para este fin el estimador de Hakulinen7, si bien, dado que el tiempo de seguimiento no fue demasiado largo (no más de 10 años), es de esperar que los resultados obtenidos por otros estimadores para la supervivencia relativa serían similares8.
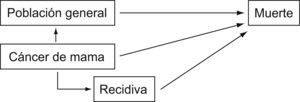
En la figura 1 puede verse de forma esquemática el procedimiento seguido. Se seleccionó la población objetivo teniendo en cuenta que una población con características generales (edad y sexo) similares a las del estudio también es una población en riesgo.
Todos los análisis estadísticos se realizaron con el software de difusión libre R.2.6.1 (www.r-project.org). Para el cálculo de la supervivencia relativa se usó el paquete relsurv desarrollado por Pohar y Stare9.
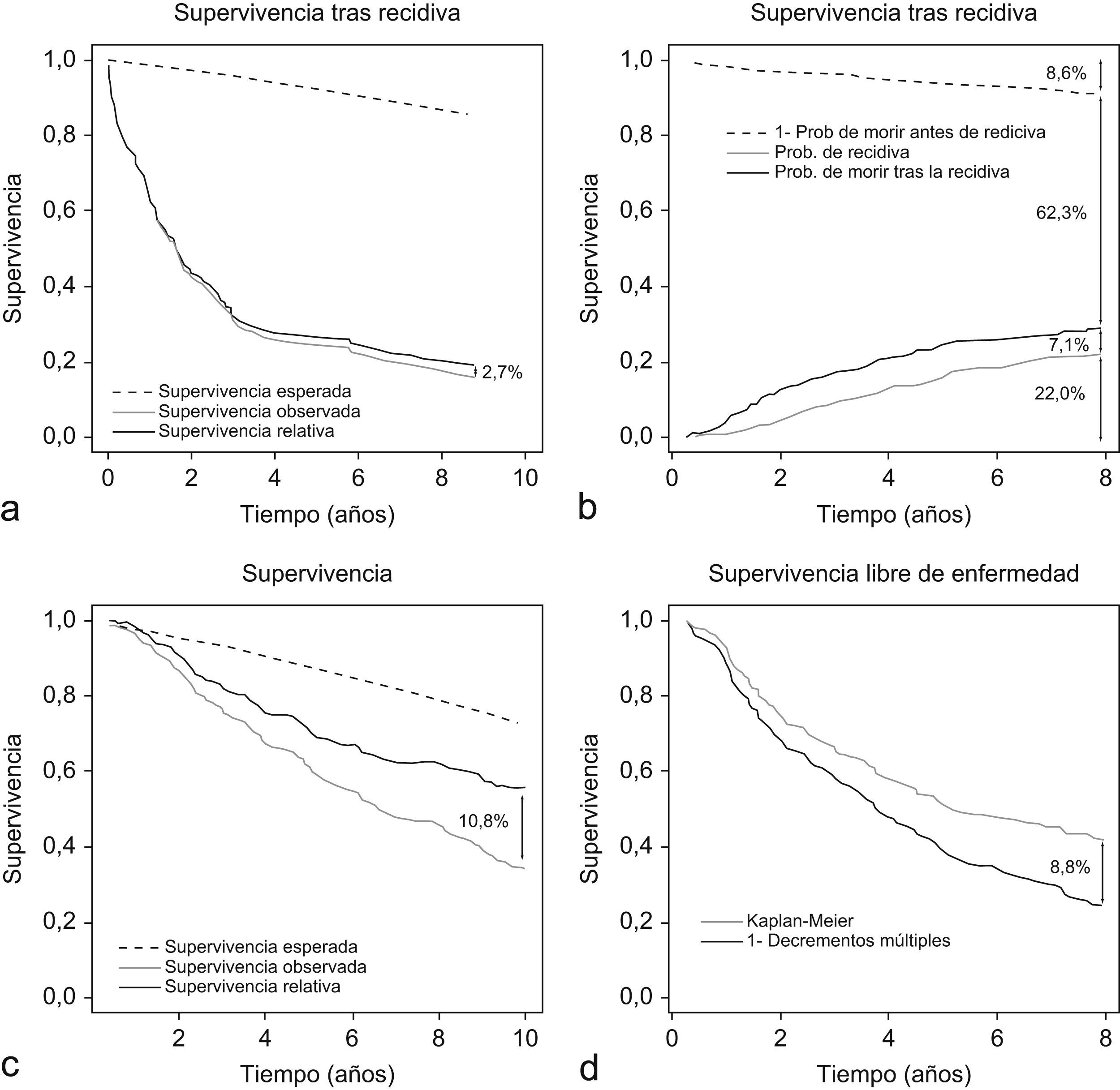
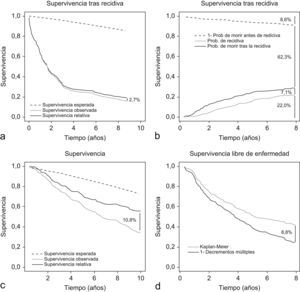
ResultadosAl considerar el tiempo libre de enfermedad se comprobó que al asumir como censurados los tiempos de las mujeres que fallecieron antes de la recidiva (esta hipótesis implica que no se sabe si en el futuro se va a presentar recidiva o no, lo cual obviamente es incierto; censura informativa) se sobrestimaba la proporción de recidivas. La probabilidad de recidiva a los ocho años estimada por el método de Kaplan-Meier era del 37,9%, mucho mayor que la estimada con el método de los decrementos múltiples, que era del 29,1% (fig. 2d). Utilizando el primer método se derivaría que a los cinco años habría recidivado el 30,6% de las mujeres, mientras que con el segundo este porcentaje desciende al 24,5%.
Cuando se amplía el método de los decrementos múltiples al estudio de un suceso secundario y se pasa a estudiar la probabilidad de muerte después de la recidiva, se obtiene que solamente un 7,1% de las mujeres siguen vivas tras haber sufrido recidiva a los ocho años del diagnóstico. Considerando el estimador de decrementos múltiples para calcular la probabilidad de morir antes de la recidiva, se puede derivar de forma secundaria la probabilidad de vivir sin recidiva (fig. 2a y b), resultando en este caso que el 62,3% de las mujeres están en esta situación a los ocho años (todas menos el porcentaje de mujeres muertas antes de la recidiva [8,6%] y el porcentaje de mujeres con recidiva, muertas o vivas [29,1%]).
En el estudio de la supervivencia (fig. 2c y d) se observó que, a los 10 años, la supervivencia esperada de la población era del 86,2%. La supervivencia estimada mediante el estimador de Kaplan-Meier era del 67,1%. La supervivencia relativa fue, por tanto, del 77,9%. La diferencia entre ambos estimadores supera el 10,0%. Estas diferencias también fueron muy amplias al considerar globalmente las curvas de supervivencia. Cabe señalar que el 75,0% de la población superó los 10 años de supervivencia relativa, mientras que este valor no llegó a seis años y siete meses (6,5 años) al considerar la supervivencia observada.
Finalmente, al estudiar el tiempo de supervivencia (relativa y observada) después de producirse la recidiva (lógicamente sólo se consideran las 145 mujeres con recidiva) se observó (fig. 2a) que la muerte se producía en un espacio de tiempo (el 70% durante los tres primeros años) en el cual la probabilidad de muerte de la población general es muy pequeña (la edad media de las mujeres es de 57,4 años, con una desviación típica de 14,5), por lo que ambas curvas consideradas están muy próximas. La supervivencia relativa al final del periodo fue del 18,7%, frente al 16,0% la observada. Lógicamente, también fueron muy pequeñas las diferencias en el tiempo mediano de supervivencia: 1,7 años (1,2–2,4) para la supervivencia relativa y 1,6 años (1,2–2,3) para la observada.
ConclusionesEn este trabajo se ilustra el uso del método de los decrementos múltiples en un estudio real sobre el tiempo hasta la recidiva en las mujeres con cáncer de mama en la provincia de Gipuzkoa. Se comprueba que al usar los estadísticos implementados en los paquetes estadísticos usuales, la sobrestimación del porcentaje de recidivas a los ocho años es del 8,8%. Estos resultados son similares a los obtenidos, con datos simulados, por Llorca et al5. Por otro lado, Gonseth et al11, bajo ciertos supuestos, determinan que la probabilidad de que una mujer de Castilla-La Mancha muera por cáncer de mama antes de los 75 años de edad es del 1,53%, y este porcentaje se reduce al 1,14% si se ajusta por riesgos competitivos. Asimismo, la mortalidad observada a los 10 años en las mujeres con la enfermedad es un 10,8% mayor que la relativa (que tiene en cuenta la mortalidad poblacional). Estos datos también concuerdan con los de otros estudios similares (véase por ejemplo el de Larrañaga et al6 y las referencias en él citadas).
Consideramos que al realizar un análisis del tiempo necesario para que un determinado evento (muerte, recidiva) suceda en una población determinada (mujeres diagnosticadas de cáncer de mama) se debe prestar especial atención en las hipótesis previas requeridas por las técnicas usadas (hipótesis de proporcionalidad de los riesgos en la regresión de Cox10, entre otros). Un claro ejemplo de estos descuidos surge con las hipótesis que las censuras deben satisfacer para que el estimador de Kaplan-Meier converja a la función de supervivencia real (deben ser no informativas e independientes del tiempo de supervivencia). Esta asunción se viola cuando, al estudiar el tiempo hasta la recidiva, se consideran como censuradas aquellas personas que mueren antes de que el evento suceda (censura informativa y dependiente del tiempo de supervivencia), suponiendo que se desconoce el tiempo real hasta la recidiva del sujeto, cuando en realidad se sabe que esas personas no van a recidivar, lo que provoca una sobrestimación de la probabilidad de recaída.
Por otro lado, en el estudio del tiempo de supervivencia es necesario tener en cuenta cuál es el comportamiento de la población general de referencia (tasas de mortalidad), e incorporar esta información en el análisis. Como es lógico, este factor cobra especial importancia en enfermedades que aparecen a edades avanzadas, ya que el riesgo de mortalidad por otras causas crece considerablemente, lo que hace aún más necesario el uso de técnicas alternativas, como el método de los decrementos múltiples. La metodología de riesgos competitivos ha sido ampliamente utilizada, por ejemplo para el ajuste del riesgo de morir por cáncer de mama11.
Si bien el cálculo de la supervivencia relativa no es estándar en los paquetes estadísticos más usuales (SPSS, StatGraphics, Statistica…), hay funciones en SAS, Stata, R, etc., y diversos software específicos (RELSURV 2.012 y WAERS13, entre otros) que facilitan su cómputo; su uso está bastante generalizado en los estudios de supervivencia de cáncer6,7 y se empiezan a utilizar habitualmente en otras enfermedades14.
En los últimos tiempos, numerosos estudios abordan el análisis de supervivencia haciendo énfasis en los estados intermedios antes de la consecución final del evento (problemas multiestado), y desde distintos puntos vista15. Asimismo, la proliferación de implementaciones en distintas aplicaciones16,17 (con especial mención a los diferentes paquetes aparecidos para el software libre R9,16) de estas funciones hace posible la generalización de su empleo en la práctica bioestadística, con la consiguiente mejora en la calidad de los resultados.
Los autores desean agradecer a los tres revisores anónimos sus comentarios y sugerencias, que indudablemente han ayudado a mejorar el trabajo.