Adequate physical activity levels and a healthy lifestyle may prevent all kinds of non-communicable diseases, promote well-being and reduce health-care costs among perimenopausal women. This study assessed an exercise programme for perimenopausal women.
MethodA total of 150 women (aged 45-64 years) not engaged in regular physical activity were randomly assigned to either a 16 week exercise intervention or to the control group. The study was conducted from the perspective of the National Health System. Health outcomes were quality-adjusted life years (QALYs), measured by the EuroQol-5D-5L questionnaire. The total direct costs of the programme were the costs of visits to primary care, specialty care, emergency, medicines, instructor cost and infrastructure cost. The results were expressed as the incremental cost-effectiveness ratio. Sensitivity analysis was undertaken to test the robustness of the analysis.
ResultsMean QALYs over 16 weeks were.228 in the control group and.230 in the intervention group (mean difference: .002; 95% confidence interval [95%CI]: −0.005 to 0.009). Improvements from baseline were greater in the intervention group in all dimensions of the EuroQol-5D-5L but not statistically significant. The total costs at the end of the intervention were 160.38 € in the control group and 167.80 € in the intervention group (mean difference: 7.42 €; 95%CI: −47 to 62). The exercise programme had an incremental cost-effectiveness ratio of 4,686 €/QALY.
ConclusionsThe programme could be considered cost-effective, although the overall difference in health benefits and costs was very modest. Longer term follow-up is needed.
El ejercicio físico puede promover el bienestar y reducir los costes de atención médica en las mujeres perimenopáusicas. Este estudio evalúa un programa de ejercicio físico en mujeres perimenopáusicas.
MétodoUn total de 150 mujeres (de edades comprendidas entre 45 y 64 años) fueron asignadas aleatoriamente al grupo de intervención o al grupo de control. El estudio ha tenido una duración de 16 semanas. Los resultados en salud se han medido en años de vida ajustados por calidad (AVAC) mediante el cuestionario EuroQol-5D-5L. Se ha considerado el total de costes directos del programa, integrado por los costes de las visitas en atención primaria, atención especializada y urgencias, medicamentos, coste del monitor y coste de las instalaciones. Los resultados se han expresado como ratio coste-efectividad incremental. La robustez del modelo se ha contrastado con un análisis de sensibilidad.
ResultadosAl final de la intervención, los AVAC fueron 0,228 en el grupo de control y 0,230 en el grupo de intervención (diferencia media: 0,002; intervalo de confianza del 95% [IC95%]: −0,005 a 0,009). La mejoría fue mayor en el grupo de intervención en todas las dimensiones del EuroQol-5D-5L, pero sin significación estadística. Los costes totales al finalizar la intervención han sido de 160,38 € en el grupo de control y 167,80 € en el de intervención (diferencia media: 7,42 €; IC95%: −47 a 62). El programa de ejercicio físico ha tenido una ratio coste-efectividad incremental de 4686 €/AVAC.
ConclusiónEl programa debe considerarse coste-efectivo, aunque la diferencia en resultados de salud y costes ha sido muy moderada. Se necesita un seguimiento a más largo plazo.
Menopause is defined by the World Health Organization as the last day of menstruation which is due to the loss of ovarian follicular activity. It occurs on average around the age of 51.1 Perimenopause is an imprecise period that begins with the first alterations of the ovarian cycle and ends one year after the last menstruation.1 Symptoms associated with perimenopause can be quite varied: vasomotor symptoms such as hot flushes,2 bone loss which can lead to osteoporosis,3 bodily changes such as increased waist circumference, increased adipose tissue, decreased muscle tissue4 or even increased risk of heart disease.5,6 Many of these changes experienced during perimenopause can be made more bearable or even prevented by healthy lifestyle habits.7,8
Numerous studies demonstrate the positive impact of physical activity or exercise on diminishing risk factors associated with cardiovascular disease,9,10 promoting weight loss11 and preventing bone loss or osteoporosis.12 In addition, women suffering symptoms of menopause tend to use more medication and other health care.13,14 Although the health benefits of physical activity are strongly established, the prevalence of physical activity in midlife women use to be inadequate, and evidence remains inconclusive on the role of physical activity on menopausal symptoms.15,16 Our hypothesis is that a physical exercise program will improve quality of life at an acceptable cost. Even though menopause is a phenomenon that ultimately concerns all women, only three previous studies have examined the cost-effectiveness of a physical exercise program in women around the age of menopause.17–19 All studies concluded that the physical exercise program for targeted women was cost-effective.
The randomized control trial Fitness League Against MENopause COst (FLAMENCO)20 investigated symptoms, health related quality of life (HRQoL) and costs of a physical exercise program (Trial Number NCT02358109, https://clinicaltrials.gov/ct2/show/NCT02358109, date of registration: September 23, 2014). The objective of this article is to study the cost-effectiveness of the physical exercise program for perimenopausal women, measured in terms of cost per quality-adjusted life years (QALYs), which was the primary outcome of the study.
MethodsThe study was designed as a randomized controlled trial and was carried out over a period of 16 weeks from the beggining of March to the end of June 2015 at a primary care center. The study population were women from Granada (Spain) who were not engaged in regular physical exercise, but otherwise healthy and able to exercise, aged between about 45 to 60 years coinciding with the perimenopausal period. They were randomly assigned to either an exercise intervention group (N = 74) or to control group (N = 76). Both groups received four conferences in which general advice about the positive effects of a physical exercise program and of the Mediterranean diet were given. The exercise intervention was performed in four groups. The groups trained 3 days/week (60minutes/session) for a 16-week period at the primary care centre. Each exercise included a 10-minute warm-up period with walks and mobility exercises, followed by 40-minute of a main part which varied across week days. Sessions finished with a 10-minute cool-down period of stretching and relaxation exercises. The weekly program of exercises consisted of resistance strength on Monday, balance oriented activities on Wednesday and combination of aerobic, resistance strength and coordination exercises on Friday. Outcome assessors and data analysts were blinded to the allocation. Full details of the Flamenco project design and methodology are described elsewhere.20
The study followed the Consolidated Health Economic Evaluation Reporting Standards (CHEERS)21 and recommendations for economic evaluation applied to health technologies in Spain.22 The study was approved by the Ethics Committee for Research Involving Human Subjects at the University of Granada and was conducted from the perspective of the National Health System. The participants provided written informed consent to participate. A literature review was conducted to identify other economic evaluations in this area (see Additional material online for search terms).
Health care resource use (visits to primary care, speciality care and emergency rooms) and pharmaceutical consumption of each patient before and during the study was obtained through medical history from Diraya system23 used by the Public Health System of Andalusia.
Costs were calculated at 2015 prices. The salary cost of the instructor in charge of carrying out the exercise program was 8.74 €/hour.24 Assuming 12hours/week of instructor‘s work (four groups, 3hours/week/group) and 16 weeks of intervention, the personnel cost of the exercise program/woman was (8.74 €/h × 12h/week × 16 weeks) / 74 women = 22.68 €/woman. Prices per visit in primary care, speciality care and emergency services were estimated from standard health service costs of 200525 and updated for inflation to 2015 prices.26 The consumption cost of prescribed pharmaceuticals was calculated based on the prices, prescribed dose and schedule of administration in Diraya.
In the clinical study, the exercise program facilities were provided by the health service at no financial cost. In practice in other settings there may be a financial cost or an opportunity cost (another activity that is displaced by the exercise program). We assumed the cost of hiring a suitable facility in Granada for carrying out the exercise program would be 500 €/month based on market prices in 2015 in Granada, and the cost of utilities (cleaning, lighting, power, etc.) would be 165 €/month.27 Assuming a maximum utilization of 55hours/week (238hours/month), and a group size of 18 women, the infrastructure cost per woman per hour is 0.16 €, calculated as (500 + 165) / (238 × 18).
The HRQoL was measured by the Spanish version of EuroQol-5D-5L (EQ-5D-5L). The questionnaire was completed at the beginning, at the middle and at the end of the study. Utility was estimated using the published tariff.28 QALYs were calculated as the area under the curve. A random effects ordered logistic model (xtlogit command in Stata) was used to measure the difference in each dimension of EQ-5D-5L between groups.
Missing data can lead to biased estimates and reduced precision. Bias may be especially likely when there is a big difference in missing data between groups. Because resource use data were collected from primary care records, there were no missing cost data. However, there were missing EQ-5D-5L data at baseline, 8 weeks and 16 weeks. Baseline data were imputed with the mean of the group.29 Missing intermediate and final EQ-5D-5L index scores were imputed using multiple imputation with chained equations. The multiple imputation missing data model included as predictive variables EQ-5D-5L indices at baseline and follow-up, costs and age. First, the missing data were imputed under the missing at random (MAR) assumption. This was the main analysis (base-case). Second, complete case analysis was performed which would correspond to a scenario where women who completed all follow-up can be considered fully representative of all the women who initially agreed to participate. This assumes data are missing completely at random (MCAR). The third scenario considered what might occur if data were missing not at random (MNAR or informative missingness). In this paper, a simple pattern mixture model was implemented, following the approach recommended in Faria et al.29 For example, the MNAR model allows for the possibility that the probability of attending follow-up was related (either positively or negatively) to the health of the women at that time. The imputed EQ-5D-5L of the women who did not return a questionnaire at 4 months were modified in 1% variations above (below) the value predicted by MAR. This corresponded to a scenario where women that fail to attend the exercise program were more (less) healthy than average. The aim was to search for the threshold increment in EQ-5D-5L above the value predicted by MAR which changed the decision at the commonly-used willingness-to-pay (22,000 €/QALY).30
Incremental cost and QALYs were calculated using bivariate regression (sureg command in Stata). QALYs were adjusted for baseline EQ-5D-5L31 to account for differences between groups at baseline. Coefficients were combined across the multiple imputed dataset using Rubin's rules.29 The probability that the intervention was cost-effective was calculated assuming the data were bivariate normal distributed.32 The analyses were performed using STATA 14.
To assess the robustness of the results additional sensitivity analysis was performed, alongside the missing data models described above. The first model, the main analysis, uses multiple imputation assuming missing data are MAR and includes infrastructure costs. In the second model we removed the infrastructure cost. In the third model (complete case) we removed all the women who did not return a HRQoL questionnaire (assuming missing data are MCAR). The fourth model excludes the infrastructure costs and also all those women who did not return the questionnaire. Fifth, the assumption that missing data are MNAR was used to find the threshold of improvement in non-attending women‘s health that makes the model not cost-effective.
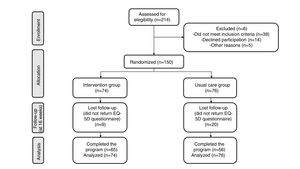
ResultsOf the 150 women who participated in the study, 76 (51%) were in the control group and 74 (49%) were in the intervention group. No significant differences in baseline variables were found between groups (Table 1). Figure 1 shows the Consort flow diagram.
Baseline characteristics of intervention and control groups.
| Intervention group(N = 74) | Control group(N = 76) | p | |
|---|---|---|---|
| Age, years (mean, SE) | 54.0 (0.52) | 53.22 (0.88) | 0.45a |
| Education | 0.99c | ||
| No education (frequency, %) | 2 (2.74) | 2 (2.63) | |
| Primary (frequency, %) | 18 (24.66) | 21 (27.63) | |
| Secondary (frequency, %) | 16 (21.92) | 15 (19.74) | |
| Professional experience (frequency, %) | 12 (16.44) | 14 (18.42) | |
| Bachelor (frequency, %) | 15 (20.55) | 13 (17.11) | |
| Master (frequency, %) | 10 (13.70) | 11 (14.47) | |
| Regular or occasional smoker | 0.16c | ||
| Daily smoker (frequency, %) | 12 (16.67) | 16 (21.62) | |
| Occasional smoker (frequency, %) | 7 (9.72) | 2 (2.7) | |
| Former smoker (frequency, %) | 38 (52.78) | 33 (44.59) | |
| Never have smoked (frequency, %) | 15 (20.83) | 23 (31.08) | |
| Civil status | 0.33c | ||
| Married (frequency, %) | 50 (68.49) | 56 (73.68) | |
| Single (frequency, %) | 10 (13.70) | 7 (9.21) | |
| Separated (frequency, %) | 7 (9.59) | 3 (3.95) | |
| Divorced (frequency, %) | 4 (5.48) | 9 (11.84) | |
| Widow (frequency, %) | 2 (2.74) | 1 (1.32) | |
| Employment (frequency, %) | 36 (49.32) | 44 (59.46) | 0.19c |
| Children (mean, SE) | 1.95 (0.12) | 1.99 (0.11) | 0.80a |
| Use of health-care services in the previous 8 weeks (mean, SE) | |||
| Visits to a primary care | 0.93 (0.13) | 0.70 (0.12) | 0.17a |
| Visits to a specialist | 0.25 (0.07) | 0.19 (0.05) | 0.50a |
| Visits to an emergency | 0.07 (0.03) | 0.04 (0.02) | 0.54a |
| Medication cost in previous 8 weeks (median, IQR) (€) | 8.70 (22.86) | 7.58 (21.73) | 0.92b |
| EQ-5D-5L index score (between 0 and 1) (mean, SE) | 0.839 (0.02) | 0.854 (0.01) | 0.53b |
EQ-5D-5L: EuroQol-5D-5L; IQR: interquartile range; SE: standard error.
The average total cost per woman was slightly higher in the intervention group than in the control group but the difference was not significant (167.80 € and 160.38 €, respectively; difference: 7.42; p = 0.8, 95% confidence interval [95%CI]: −47 to 62) (Table 2). The intervention cost per person was 30.36 € (22.68 € instructor and 7.68 € infrastructure), representing 18% of total costs in the intervention group, but this was partly compensated for by less use of healthcare services. Excluding the intervention cost, total direct costs were 16.7% lower in the intervention group than in the control group (137.45 € and 160.38 €, respectively; difference: −22.94; p = 0.38; 95%CI: −75 to 29). However, differences were not statistically significant (Table 2).
Costs of intervention group and control group.
| Unit cost (€) | Resource use | Mean cost/person | Total costs/person | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 8-0 weeks | 0-8 weeks | 8-16 weeks | 8-0 weeks | Diff. mean cost per person (€) | 0-8 weeks | Diff. mean cost per person (€) | 8-16 weeks | Diff. mean cost per person (€) | 0-16 weeks | Diff. mean cost per person (€) | |||||||||
| C | I | C | I | C | I | C | I | C | I | C | I | C | I | ||||||
| Primary care (visits) (number of patients >0) | 21.62 | 71 | 52 | 60 | 59 | 51 | 39 | 20.20 | 15.19 | −5.01 | 17.07 | 17.24 | 0.17 | 14.51 | 11.39 | −3.11 | 31.58 | 28.63 | −2.94 |
| 44 | 34 | 35 | 30 | 33 | 27 | ||||||||||||||
| Specialist (visits) (number of patients >0) | 62.74 | 19 | 14 | 33 | 22 | 33 | 24 | 15.69 | 11.87 | −3.82 | 27.24 | 18.65 | −8.59 | 27.24 | 20.35 | −6.89 | 54.48 | 39.00 | −15.48 |
| 13 | 12 | 22 | 15 | 25 | 17 | ||||||||||||||
| Emergency rooms (visits) (number of patients >0) | 59.58 | 5 | 3 | 7 | 7 | 14 | 6 | 3.92 | 2.42 | −1.50 | 5.49 | 5.64 | 0.15 | 10.98 | 4.83 | −6.14 | 16.47 | 10.47 | −6.00 |
| 4 | 3 | 7 | 6 | 12 | 5 | ||||||||||||||
| Medicine | 18.59 | 27.50 | 8.90 | 26.52 | 29.02 | 2.49 | 31.34 | 30.33 | −1.01 | 57.86 | 59.35 | 1.49 | |||||||
| Total costs | 58.40 | 56.98 | −1.42 | 76.32 | 70.55 | −5.77 | 84.07 | 66.90 | −17.17 | 160.38 | 137.45 | −22.94e | |||||||
| Costs of the intervention | |||||||||||||||||||
| Instructor | 8.74 | 0 | 0 | 0 | 96 h | 0 | 96 h | 0.00 | 0.00 | 0.00 | 11.34 | 0.00 | 11.34 | 0.00 | 22.68 | ||||
| Infrastructure | 0.16 | 0 | 0 | 0 | 24 h | 0 | 24 h | 0.00 | 0.00 | 0.00 | 3.84 | 0.00 | 3.84 | 0.00 | 7.68 | ||||
| Total costs | 58.40 | 56.98 | -1.42a | 76.32 | 85.73 | 9.41b | 84.07 | 82.08 | -1.99c | 160.38 | 167.80 | 7.42d | |||||||
C: control group (N = 76); Diff.: difference; I: intervention group (N = 74).
There may be differences in direct costs and in total costs as a result of rounding out.
Number of patients >0 refers to patients attending primary care, speciality care or emergency rooms.
8-0 weeks refers to eight weeks before the start of the study.
All p-values were calculated by bootstrap method.
Supplementary Table I online contains the responses to the various items of EQ-5D-5L for each group. The unadjusted utility was higher in the intervention group than in the control group at the end of the study (Supplementary Table II online). However, there were small differences in EQ-5D-5L score between groups baseline. Although these were not statistically significant, these differences can affect the results of a cost-effectiveness analysis because baseline EQ-5D-5L is an element of the calculation of QALYs. Once adjusted for the difference that existed between the two groups at baseline,31 and imputing for missing data, the difference in QALYs was 0.002 (p = 0.66; 95%CI: −0.005 to 0.009). The incremental cost-effectiveness ratio (ICER) was 4,686 €/QALY (Table 3).
Sensitivity analysis.
| Model | Costs | Difference | QALYs | Difference | ICERa | ||
|---|---|---|---|---|---|---|---|
| Intervention | Control | Intervention | Control | ||||
| 1. Multiple imputation model (base-case) | 167.80 | 160.38 | 7.42 | 0.2295 | 0.2279 | 0.0016e | 4,686 |
| 2. Multiple imputation without infrastructure costsb | 160.12 | 160.38 | -0.26 | 0.2295 | 0.2279 | 0.0016 | Intervention dominates |
| 3. Complete case analysisc | 153.15 | 168.53 | -15.37 | 0.2304 | 0.2272 | 0.0032 | Intervention dominates |
| 4. Complete case analysis without infrastructure costs | 145.47 | 168.53 | -23.05 | 0.2304 | 0.2272 | 0.0032 | Intervention dominates |
| 5. Increased QALYs of all individuals with imputed utilities by 2%d | 167.80 | 160.38 | 7.42 | 0.2300 | 0.2293 | 0.0007e | 10,748 |
ICER: incremental cost-effectiveness ratio; QALYs: quality adjusted life years.
ICER is the result of dividing the difference between costs and QALYs, both without rounding out. In model 1 that is 7.416473/0.0015827, and in model 5 that is 7.416473/0.00069.
Infrastucture costs refers to the cost of hiring a suitable facility and to the cost of utilities as cleaning, power, etc.
The sensitivity analysis are shown in Table 3. In model 2, the total mean costs in the intervention group were lower and delivered an improvement in health, so that the physical exercise program is said to “dominate” usual care. The results of the first two models were different, due to the small difference in QALYs between the two groups. This means that a small change in costs had a large impact on the ICER. In models 3 and 4 the result was similar to model 2, i.e. the intervention was dominant (Table 3). Model 5 assumes a scenario where women might not attend follow-up for reasons related to their health on that day, that is, missing data were MNAR. It was found that the exercise program starts to be not cost-effective if the imputed EQ-5D-5L of the women who did not return a questionnaire at 4 months was 3% greater than the value predicted by MAR, that is, if it is assumed that women who did not attend were 3% more healthy than would be expected by their age, use of health services and other characteristics. Table 4 shows the results of the MNAR analysis.
Association of quality-adjusted life years and incremental-cost effectiveness ratio with non-attending women's health.
| Non-attending women's health at 16 weeks of follow-up | 96% | 97% | 98% | 99% | 100% | 101% | 102% | 103% | 104% |
|---|---|---|---|---|---|---|---|---|---|
| Difference in cost (mean, SD) | 7.42 (27.71) | 7.42 (27.71) | 7.42 (27.71) | 7.42 (27.71) | 7.42 (27.71) | 7.42 (27.71) | 7.42 (27.71) | 7.42 (27.71) | 7.42 (27.71) |
| Difference in QALYs (mean, SD) | 0.0034 | 0.0029 | 0.0025 | 0.0020 | 0.0016 | 0.0011 | 0.0007 | 0.0002 | −0.0002a |
| (0.0036) | (0.0036) | (0.0036) | (0.0035) | (0.0035) | (0.0036) | (0.0036) | (0.0036) | (0.0037) | |
| ICER (€/QALY) | 2,202 | 2,538 | 2,996 | 3,655 | 4,686 | 6,526 | 10,748 | 30,438 | −36,590 |
ICER: incremental cost-effectiveness ratio; QALYs: quality-adjusted life years; SD: standard deviation.
All differences in QALYs are rounded out.
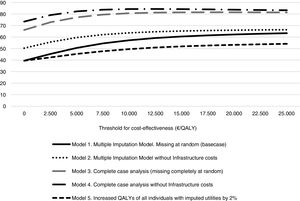
The probability that the intervention was cost-effective in different scenarios and at different levels of willingness to pay is shown in Figure 2. The probability of being cost-effective when the threshold is 25,000 €/QALY was 63% in model 1, 66% in model 2, 81% in model 3, 83% in model 4 and 54% in model 5.
DiscussionThe base case for this study found that the cost per QALY of a physical exercise program was 4,686 €/QALY. The mean QALYs over 16 weeks were 0.230 vs. 0.228 (p = 0.66) and costs were 167.80 € vs. 160.38 € (p = 0.8) in the intervention and control group, respectively. There is no official cost per QALY threshold in Spain but some authors have recommended that interventions with an ICER 22,000-25,000 €/QALY should be accepted.30
The intervention cost per person was 30.36 €, but this was partly compensated for by less use of other healthcare services in the intervention group, especially in specialist visits. This supports results from other studies that physically active people tend to use less health-care services.33 Unexpectedly, specialist visits increased from baseline in both groups, but considering the waiting list, the appointments could have been agreed even before the beginning of the study. That is, we cannot conclude that women's health worsened and for that reason they went more often to the specialist. Also unexpectedly, use of medication increased in control group from baseline. Healthcare can be very variable, so it is difficult to draw inferences.
Other studies have shown physical activity improves quality of life.34,35 The trial protocol considered for the power calculation that the clinically meaningful change in EQ-5D-5L index over 16 weeks should be 0.07 units.20 The actual change in EQ-5D-5L in the intervention group between baseline and 16 weeks was 0.039 units, which is still substantial, but there was also a similar improvement in the control group. These improvements in health in the control group may be because the control group received more than usual care, as both groups underwent fitness testing at baseline and follow up, and received recommendations on exercise and its benefits for the longevity, prevention and treatment of diseases, as well as the benefits of the Mediterranean diet. These costs were not taken into account for the calculation of total costs, because they were identical in both groups.
The current study is one of the few cost utility analyses of an exercise intervention program with perimenopausal women. What makes our study unique is that the exercise program was especially designed for perimenopausal women. One of the limitations of this study was that 20% of women did not complete questionnaires at the end of the study. However, this rate of withdrawal was allowed for in the sample size calculation.20 Resource use and costs were available for all participants from administrative data. Furthermore, we have taken account of missing quality of life data in the analyses using a published methodology.29 Results are generally robust to assumptions about missing data. The incremental cost-effectiveness ratio was less than 22,000 €/QALY in all scenarios tested in sensitivity analysis. Infrastructure costs are uncertain, but are not likely to influence the overall result. However, the decision is very sensitive to assumptions about the true values of the missing data. It appears not to be cost-effective under the scenario that women who did not attend follow-up were 3% more healthy than would be expected given their age and other characteristics. This result occurs because more women failed to attend follow-up in the control group than the exercise group. We should also consider that these women might not be fully representative of the perimenopausal population, since women who practiced physical activity regularly were excluded from the study. Although the exercise program might be considered cost-effective on average, the difference in improvement in health between intervention and control group is very small and statistically not significant.
Three other studies have investigated the cost-effectiveness of an exercise program in perimenopausal women. Kolu et al.17 evaluated a program in Finland where 151 women aged 40-63 years were divided into a control group and intervention group. The intervention group underwent a 6-month exercise program 4 times/week for 50minutes. The mean difference in costs was 53 €. However, the study did not report the difference in QALYs over 6 months. Instead, they reported a crude projection, assuming that the difference in HRQoL at the end of the study would be maintained for the rest of the patient's expected life. Using this projection, the reported mean difference in QALYs over the patient's lifetime was 1.16, with an ICER of 46 €/QALY. However, this extrapolation seems highly optimistic and is therefore likely to be biased. The failure to report actual outcomes at 6 months means we cannot compare this result with our study.
Another study conducted in Cáceres, Spain, assessed the cost-effectiveness of an exercise program where 106 women aged 60 years and older participated.18 The intervention group underwent a 6-month walking-based supervised exercise program with three 50-minute sessions/week. The control group received a recommendation of physical activity. The difference in cost was 41 € (no p-value given) and the difference in QALYs at six months was 0.132 (95%CI: 0.104 to 0.286) therefore the ICER was 311 €/QALY gained. This is a much greater health benefit than found in our study. However, the study population is older and more unfit than our study and so results may not be generalizable.
Goranitis et al.19 evaluated the cost-utility of an individual and a social version of an exercise intervention relative to a control group in West Midlands, United Kingdom, with 261 women aged between 48 and 57 years. Both intervention groups followed a 6-month course of moderate intensity aerobic exercise for 30minutes on at least 3 days/week. The difference found in QALY at 12 months of 0.013 (95%CI: −0.010 to 0.036) in exercise support versus control, and a very small difference in cost £18 (95%CI: −68 to 105) might be considered a slightly greater health benefit than observed in our study, though still not statistically insignificant. No benefit was seen in the individual intervention group (without social support).
According to our findings, the program is cost-effective on average. However, the difference in health benefit of the intervention group compared to the control group at four months is small and statistically insignificant. Further studies in this area might consider whether a longer exercise program, or a program targeted at specific risk groups, or a program that reinforces social bonds within the group, might have more impact. The option of using another questionnaire to measure QALYs should be considered. Longer term follow up is also required.
In perimenopausal women, the irregular menstrual periods can be accompanied by hot flashes, vaginal dryness, trouble sleeping, bodily changes, bone loss or even by a higher risk of heart disease. Despite the positive impact of physical activity in health and quality of life, the number of perimenopausal women exercising regularly is inadequate.
What does this study add to the literature?After 16 weeks of specialized physical exercise program, the intervention group improved more than the control group, but the differences were not statistically significant. The cost of the program is relatively small. According to this study, policy makers should consider financing this exercise program. Further research should focus on longer follow-up and if a more targeted approach would offer better value-for-money.
Miguel Ángel Negrín Hernández.
Transparency declarationThe corresponding author on behalf of the other authors guarantee the accuracy, transparency and honesty of the data and information contained in the study, that no relevant information has been omitted and that all discrepancies between authors have been adequately resolved and described.
Authorship contributionsZ. Špacírová contributed to acquisition of data, analyzed and interpreted data and wrote the article. D. Epstein analyzed and interpreted data, contributed to design of the study and to revising the manuscript critically. L. García Mochón contributed to design of the study. V. Aparicio contributed to acquisition of data. M. Borges Cosic contributed to acquisition of data. M.P. López contributed to design of the study and to revising the manuscript critically. J.J. Martín contributed to design of the study and to revising the manuscript critically. All authors gave final approval of the version to be published.
FundingThe project received funds from Consejería de Economía, Innovación, Ciencia y Empleo, Junta de Andalucía (PI-0667-2013).
Conflicts of interestNone.