Introducción
En los estudios de supervivencia se está interesado por el tiempo que transcurre desde un origen (nacimiento, inicio de tratamiento, etc.) hasta que ocurre un suceso (muerte, mejora, etc.)1. En numerosas ocasiones este suceso no es único y los sujetos pueden experimentar varios sucesos (o técnicamente fallos) que pueden ser de distinto tipo o bien tratarse de recurrencias del mismo suceso de interés. Debido a esto, los individuos con más sucesos estarán «sobrerrepresentados»2 y, por otra parte, los efectos de las variables explicativas (efectos «tratamiento») podrán ser distintos entre el primer suceso y los siguientes. Esto se traducirá en una posible dependencia entre los tiempos de recurrencia, consecuencia de dos fenómenos diferentes: la existencia de heterogeneidad individual y dependencia «serial». En la primera, los tiempos de supervivencia dependen unos de otros porque los individuos comparten una o más covariables omitidas. Esta heterogeneidad individual también se denomina fragilidad, dependencia entre individuos o falso «contagio». Por lo que respecta a la dependencia «serial», que equivaldría a la autocorrelación en series temporales, la dependencia se produce en el mismo individuo, entre sus observaciones repetidas. Como consecuencia de que el individuo presenta una conducta dinámica per se, la probabilidad de que se produzca un suceso no es independiente de que se produzca uno previo. Esta dependencia también se denomina dependencia dentro de un mismo individuo o «contagio» verdadero.
Con el fin de ilustrar el trabajo utilizaremos una cohorte prospectiva formada por todos los pacientes admitidos un mínimo de 24 h en la Unidad de Cuidados Intensivos (UCI) del Hospital Universitario Dr. Josep Trueta de Girona, durante el período comprendido entre el 15 de marzo y el 15 de junio de 19993. Se trata de un hospital público de nivel terciario, con 12 camas en la UCI, que cubre prácticamente toda la población de la provincia de Girona. Se pretende analizar los factores que determinan la incidencia de las infecciones nosocomiales en la UCI de dicho hospital. Las infecciones nosocomiales vienen definidas como las causadas por microorganismos adquiridos en el hospital, que afectan a los pacientes por un proceso diferente del de la infección, y que no estaban presentes en la admisión del paciente, ni tan siquiera en período de incubación. Entre los posibles factores de riesgo para la aparición de dichas infecciones distinguiremos los asociados a los pacientes (factores de riesgo intrínsecos, como su edad o sexo) y los relacionados con la UCI (factores de riesgo extrínsecos, como tratamiento antibiótico). El número total de sujetos incluidos en el estudio fue de 61 pacientes (42 varones y 19 mujeres), con un total de 40 infecciones nosocomiales. La variable dependiente (episodio de infección) consiste en el tiempo transcurrido entre el ingreso en la UCI hasta la aparición de la infección (originada por un microorganismo, bacteria u hongo), así como el tiempo entre el principio y el final de una infección. Obviamente los pacientes podrán presentar más de un episodio de infección. Sólo se analizaron infecciones nosocomiales originadas en la UCI, incluyéndose en la definición las infecciones comunitarias, las procedentes de otros hospitales y las procedentes de otras áreas hospitalarias. Para una explicación más detallada el lector interesado puede consultar en Barceló y Saez3.
El objetivo principal de este artículo es presentar una revisión de la aproximación marginal y condicional en el análisis de supervivencia multivariante. Adicionalmente, y como ilustración, se presenta una aplicación a datos reales que permite valorar la utilidad de tales aproximaciones.
Métodos
Con el propósito de solucionar los problemas ocasionados por la existencia de más de un tiempo de supervivencia por individuo, el modelo de Cox de riesgos proporcionales fue generalizado y situado en el contexto mucho más general de los modelos de intensidad multiplicativos para procesos contadores multivariantes, a través de la aproximación de Andersen y Gill (modelo AG)4-8. En la aproximación AG cada sujeto es tratado como un proceso contador con sucesos múltiples y con «incrementos» (es decir, los tiempos entre acontecimientos sucesivos) independientes, dada la «historia» de todas las variables observables hasta el tiempo de presentación de los sucesos. Es decir, con el modelo AG el riesgo de una determinada recurrencia para un individuo sigue la hipótesis de riesgos proporcionales y no está afectado por la presentación en dicho individuo de sucesos anteriores. Dicha hipótesis, llamada de «incrementos independientes», es la hipótesis clave del modelo AG. En caso de existir alguna interrelación entre sucesos se modelizaría mediante una o más variables explicativas dependientes del tiempo9.
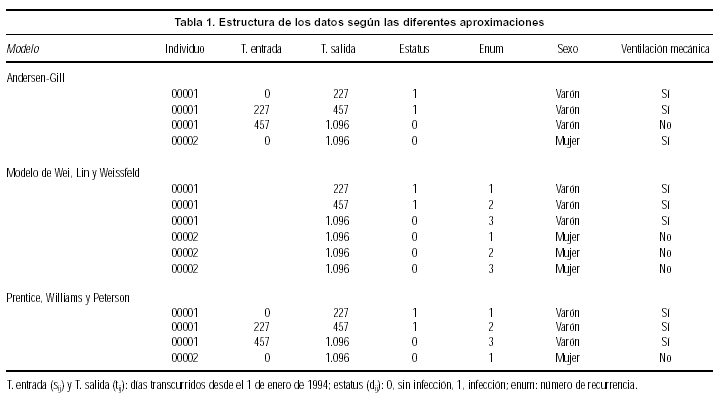
Desde un punto de vista práctico, la aproximación AG representa a cada individuo por un conjunto de observaciones sij, tij, dij, xij, kij, j = 1, ..., ni siendo (sij, tij] el intervalo de riesgo, abierto a la izquierda y cerrado a la derecha; dij = 1 si el individuo tuvo un suceso en el instante tij y 0 en otro caso; xij es un vector de variables explicativas en el intervalo, y kij denota un estrato al que puede pertenecer el sujeto durante el intervalo. Dependiendo de la escala de tiempo, la primera observación puede o no empezar en cero.
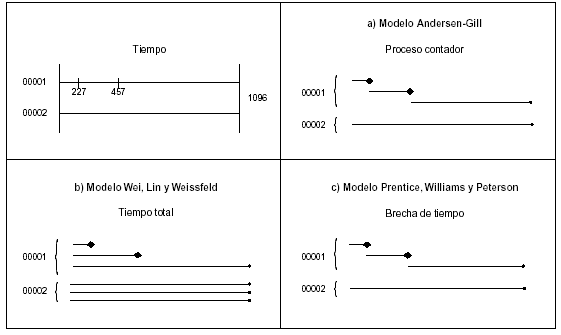
Aclararemos lo anterior mediante un sencillo ejemplo. Sean dos individuos, un varón que padeció dos episodios de infección (INF) y una mujer que no presentó ninguno (tabla 1 y fig. 1a). Los individuos se dividen en distintos registros que se corresponden con diversas bandas temporales (intervalos de observación) y cada registro es tratado como si fuesen individuos diferentes. Las bandas se construyen en función de si el individuo presenta o no un episodio de infección y de posibles cambios en las variables explicativas, no necesitando ser adyacentes. En este diseño las variables explicativas son fijas dentro de cada episodio, pero no así dentro de cada individuo (tal como suponen los modelos estándar, como el modelo de Cox de riesgos proporcionales). Nótese que es el riesgo de cada suceso concreto para un individuo determinado el que cumple la hipótesis usual de riesgos proporcionales y que el modelo supone que este riesgo no está afectado por sucesos anteriores del mismo individuo.
Figura 1. Estructura de los datos a comparar según el modelo de análisis.
La aproximación AG es sencilla, pero sus hipótesis subyacentes son muy restrictivas y pueden llegar a ser irrealizables. En concreto, no es razonable suponer, tal como hemos visto, que las bandas pertenecientes a un mismo individuo no estén correlacionadas. En la práctica esta limitación puede conducir a estimadores sesgados e ineficientes. Además, puede sobrestimarse la precisión de los estimadores puesto que, habitualmente, las observaciones de un mismo individuo suelen estar correlacionadas positivamente.
Como posible solución, a finales de los años ochenta empezaron a aparecer los modelos marginales y condicionales en el análisis de datos de supervivencia multivariante. Sin embargo, la aplicación de estos modelos aun hoy día no está muy extendida debido, principalmente, a una falta de sistematización en la bibliografía especializada. Es por ello por lo que consideramos especialmente importante describir estos modelos no sólo desde un punto de vista teórico10, sino también ilustrarlos sobre la base de datos utilizada anteriormente.
En los modelos marginales la dependencia de las observaciones puede entenderse como un «estorbo», como algo que hay que eliminar o, en todo caso, cuyos efectos se deben controlar en el análisis, pero no como objetivo en sí. Por el contrario, los modelos condicionales consideran que la dependencia puede ser también de interés por sí misma. A grandes rasgos, los modelos marginales estiman el modelo ignorando la posible dependencia entre las observaciones, aunque corrigen posteriormente la varianza «ingenua» mediante estimadores jackknife, bootstrap o «sándwich». Los modelos condicionales estiman la dependencia (o la heterogeneidad) especificando explícitamente su distribución de probabilidad e incorporándola en el modelo.
Modelos marginales
La primera aproximación marginal que comentaremos es la estimación robusta de la matriz de varianzas y covarianzas. Se parte del hecho de que la aproximación AG proporciona estimadores consistentes de los parámetros asociados a las variables explicativas. Aun así, si existe dependencia, el método proporciona varianzas sesgadas. Se trataría, por tanto, de estimar de forma robusta la matriz de covarianzas, es decir, de corregirla de forma adecuada utilizando, por ejemplo, un estimador jackknife9. La idea es sencilla, se trata de ir eliminando a un individuo de la muestra cada vez y restimar el modelo resultante. Los estimadores finales se obtienen ponderando los obtenidos tras cada una de estas eliminaciones. El problema de esta aproximación marginal estriba en que se basa en la consistencia de las estimaciones. Sin embargo, las estimaciones de los parámetros serán consistentes siempre y cuando el modelo marginal esté correctamente especificado.
Otro modelo marginal es el modelo de Wei, Lin y Weissfeld (WLW)11, en el que cada recurrencia del suceso (o tipo distinto de suceso) se modeliza como un estrato diferente, utilizándose los datos dentro de cada estrato de modo marginal. El resultado es que (todos) los individuos aparecen en todos los estratos. Es decir, el modelo WLW no es más que un modelo estratificado, siendo cada estrato una presentación del suceso de interés. Los estimadores finales son una media ponderada de los estimadores en cada estrato. Como vemos, se trata de un modelo marginal con respecto al conjunto de riesgo por cuanto el sujeto está en riesgo desde el inicio del estudio y, por tanto, no depende de sucesos previos.
Es decir, para cada una de las k recurrencias que pueda padecer un individuo i (k = 1,2,..., K), la función de riesgo puede expresarse como:
λik(t) = λi0k(t) eβ'kXik(t) t >= 0 [1]
siendo λi0k(t) (k = 1,..., K) una función de riesgo subyacente no especificada, distinta para cada recurrencia, y βk = (β1k,..., βpk)' un vector de orden p ×1 de parámetros desconocidos de la regresión.
En el modelo WLW los datos se organizan de forma diferente de la que veíamos en el modelo AG (tabla 1 y fig. 1b, en la que se ha supuesto que el máximo número de episodios de infección entre todos los individuos analizados es de tres). Nótese que cada intervalo de tiempo empieza en cero. Se trata de un modelo marginal con respecto al conjunto de riesgo por cuanto el sujeto está en riesgo desde el inicio del estudio y, por tanto, no depende de sucesos previos.
Las limitaciones del modelo WLW pueden ser superadas, en parte, utilizando la aproximación de Prentice, Williams y Peterson (PWP)12. Se trata de un modelo marginal respecto a la estimación de los parámetros, pero condicional en relación con la construcción del conjunto de individuos en riesgo. El modelo PWP permite que el riesgo basal varíe entre diferentes recurrencias. Se trata, por tanto, de un modelo de riesgos proporcionales con estratos dependientes del tiempo, en el que la dependencia entre recurrencias se controla estratificando por el número previo de presentaciones del suceso de interés. Así, a diferencia del método WLW, en el que todos los individuos están en riesgo en todo momento, el modelo PWP incluye en el conjunto de riesgo para la recurrencia k únicamente a los individuos que han experimentado k-1 recurrencias.
Prentice, Williams y Peterson12 proponen dos modelos semiparamétricos de riesgos proporcionales:
1. Tiempo desde el inicio del estudio (de tiempo total). Se incluye la función de riesgo subyacente como una función del tiempo desde el inicio del estudio
λik (t) = λ0k(t) eβ'kXik (t)[2]
2. Tiempo desde la recurrencia inmediatamente precedente (de brecha de tiempo). La función de riesgo subyacente es una función del tiempo desde la recurrencia inmediatamente precedente al tiempo de fallo:
λik (t) = λ0k (t tn(t))eβ'kXik (t)[3]
La particularidad de ambos modelos reside en que se estratifica en función del número de recurrencias previas.
Siguiendo con el ejemplo de antes, tanto para el modelo AG como para PWP los datos se organizarían tal como se muestra en la tabla 1 y la figura 1c.
Modelos condicionales
En algunos casos no sólo nos interesa el efecto marginal de las covariables sobre la función de riesgo de los tiempos de fallo de los individuos, sino también cómo los sucesos anteriores pueden influir en el riesgo de desarrollar futuros fallos. Para responder a estas cuestiones necesitamos recurrir a los modelos condicionales.
En primer lugar, la hipótesis de incrementos independientes en el modelo AG puede relajarse incluyendo en el modelo variables dependientes del tiempo, como el número de recurrencias previas, a fin de capturar la posible estructura de dependencia entre las recurrencias. En concreto, se podría trabajar con el modelo autorregresivo o markoviano. Este modelo será plenamente apropiado cuando la dependencia entre observaciones sea, principalmente, «serial». Sin embargo, y aunque es un modelo muy general, supone que la dependencia entre recurrencias decae exponencialmente y que la dependencia es idéntica para todos los individuos10.
Parte de las limitaciones anteriores pueden solucionarse mediante los modelos de fragilidad. Se trata de introducir una (modelos de fragilidad univariante) o más (modelos de fragilidad multivariante) variables aleatorias comunes a todos los individuos con el objetivo de permitir que los tiempos de supervivencia multivariantes, es decir, las observaciones repetidas de un mismo individuo, estén correlacionadas. Se trata, en definitiva, de que este efecto multiplicativo en la función de intensidad (o de riesgo) capture dos fuentes de variación distintas pero relacionadas13, con el propósito de modelar la dependencia entre los diferentes tiempos de supervivencia entre recurrencias. Una de las fuentes de variación surge de covariables comunes a todos los individuos, no observadas, las cuales, cuando se omiten, generan dependencia entre sucesos. La otra fuente de variación proviene de covariables individuales no observadas y, por tanto, no incluidas en el estudio, bien por circunstancias prácticas, bien porque no se asocian a ningún factor de riesgo de la supervivencia del individuo. Los efectos de esta fuente serían totalmente equivalentes a la dependencia serial citada en la introducción de este artículo.
Posibles alternativas para la distribución de probabilidad de la variable aleatoria fragilidad son la distribución gamma, la distribución positiva estable y la distribución gaussiana inversa, entre otras. El modelo de fragilidad gamma es el más adecuado en nuestro caso, debido, en primer lugar, al tipo de datos de que disponemos. En concreto, bajo este tipo de distribución la fuerza de la asociación entre recurrencias es estacionaria, es decir, no depende del tiempo. Este tipo de asociación es la que más se produce en el mundo real. La ventaja más importante de la distribución gamma, sin embargo, se encuentra en la facilidad analítica que permite.
En particular, el modelo AG de fragilidad14,15 puede expresarse de la siguiente manera en su caso más simple:
λi(t) = ωiYi (t) α0(t) eβ'Xi (t) [4]
siendo N = (Ni; i = 1, ..., n) un proceso contador multivariante que cuenta el número de sucesos que han ocurrido en cada uno de los n individuos en el tiempo t. Asociado a este proceso contador, existe un proceso de intensidad λcon componentes λi . El proceso Y con componentes Yi es un proceso no negativo, observable y predecible, es decir, su valor en cualquier momento t es conocido justo antes de t, indicando si un individuo i se observa en el conjunto a riesgo de experimentar un determinado suceso en el tiempo t-; α0 denota ahora una función de riesgo basal desconocida, y ωi (fragilidad) es un conjunto de variables aleatorias independientes e idénticamente distribuidas según una distribución de probabilidad paramétrica determinada, en este caso la distribución gamma, con media nula y varianza común. La variabilidad (medida por su varianza) de la fragilidad determina el grado de heterogeneidad. De hecho, cuando la varianza es igual a cero el modelo se reduce al modelo AG estándar.
El modelo descrito es un modelo muy simple, ya que asume que la fragilidad es constante a lo largo del tiempo, es decir, la fragilidad reflejaría en este caso diferencias individuales presentes al comienzo del estudio. Asimismo, este modelo supone que la fragilidad actúa proporcionalmente sobre la función basal común a todos los individuos. Al imponer esto se asume que todos los individuos siguen un patrón uniforme.
El problema es que la estimación de los parámetros del modelo utilizando directamente la máxima verosimilitud no es posible cuando la función de riesgo basal no está parametrizada, como en nuestro caso. Por otra parte, los modelos de fragilidad univariantes presentan una serie de limitaciones; entre ellas cabe destacar las siguientes: suponen que la dependencia entre observaciones es siempre positiva, no permiten la interacción entre covariables observables y la fragilidad, y más importante aún, sólo permiten la presencia de un único efecto aleatorio, siendo además éste constante a lo largo del tiempo. Con el propósito de solucionar estos problemas, Barceló y Saez16 proponen un método de especificación y estimación original basado en la verosimilitud extendida de Nelder y Lee17, así como en el método de las variables instrumentales, y estudian las ventajas analíticas de dicho método, en particular, en relación con alternativas de especificación (modelos de fragilidad multivariantes) y de estimación (algoritmo EM). De una manera muy resumida, introducen un nuevo paso en el algoritmo EM, modelizando la varianza de la fragilidad directamente. Mediante el algoritmo así modificado (algoritmo EMB), se estima no sólo el modelo de supervivencia, sino también la varianza de la fragilidad de forma simultánea. Mediante esta modificación solucionan parte de las limitaciones citadas anteriormente; en particular, permiten que la fragilidad no sea constante entre individuos. Una explicación más detallada puede encontrarse en Barceló y Saez16.
Una alternativa a los modelos de fragilidad la proporcionan los modelos de Cox penalizados18. En resumen, se trata de maximizar una función de verosimilitud parcial penalizada. El término penalizador captura la variabilidad local presente en la densidad conjunta de los datos.
Los modelos que se han comentado no están anidados, por lo que las usuales medidas de bondad de ajuste no pueden utilizarse. Como alternativa se suele emplear el criterio de información de Akaike (AIC).
El software estadístico que permite ajustar todos los modelos vistos y que, por otra parte, se ha utilizado en la aplicación práctica, es el S-PLUS 200019. En concreto, se debe utilizar la instrucción coxph, que permite considerar diferentes tipos de truncamiento y censura. La estimación robusta de la varianza se obtiene mediante la instrucción cluster. Desafortunadamente, hay pocos programas que permitan la estimación de modelos marginales y/o condicionales en el contexto multivariante. Además del S-PLUS 2000, el lector interesado puede recurrir a otros programas como R (versión libre y gratuita de S-PLUS), SAS (versión 6 o posteriores, instrucciones proc phreg, aunque no permite la estimación robusta de la varianza) y, únicamente para el modelo AG estándar, STATA (versión 5 o posteriores, instrucciones stset y stcox).
Resultados
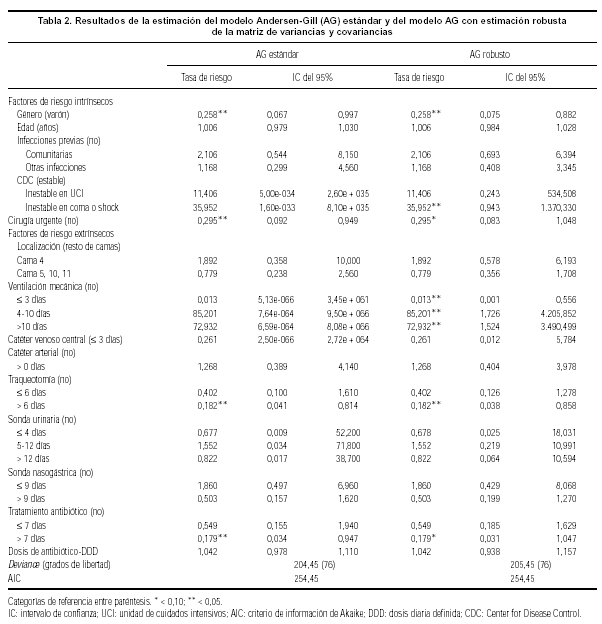
Los resultados de la estimación del modelo AG estándar aparecen en las primeras columnas de la tabla 2. En esta tabla se presentan las tasas de riesgo asociadas a toda una serie de variables explicativas y sus respectivos intervalos de confianza (IC). Por último, se ofrece una serie de medidas de bondad de ajuste del modelo. Como puede apreciarse al observar la tabla, pocas variables resultaron estar asociadas de forma significativa con el tiempo de presentación de una infección nosocomial. En concreto, ser mujer (0,258; IC del 95%, 0,067-0,997), haberse sometido a cirugía urgente (0,295; IC del 95%, 0,092-0,949), haber permanecido intubado más de 6 días mediante traqueotomía (0,182; IC del 95%, 0,041-0,814) y haber recibido tratamiento antibiótico durante más de 7 días (0,179; IC del 95%, 0,034-0,947) reducían el riesgo de tales infecciones.
Los resultados de la aplicación práctica del modelo AG con estimación robusta de la matriz de varianzas y covarianzas serían los que hemos visto anteriormente al hablar del modelo AG, ya que esta primera aproximación marginal sólo afecta a la matriz de varianzas y covarianzas, no a la construcción de los conjuntos a riesgo. Si nos fijamos en la tabla 2 y comparamos el modelo AG estándar y el modelo AG robusto, apreciamos una mayor precisión en los intervalos de confianza proporcionados por este último modelo, siendo este cambio muy significativo en variables como ventilación mecánica. Por el contrario, otras variables tales como cirugía urgente (0,295; IC del 95%, 0,083-1,048) y tratamiento antibiótico durante más de 7 días (0,179; IC del 95%, 0,031-1,047) llegan incluso a perder su significación estadística.
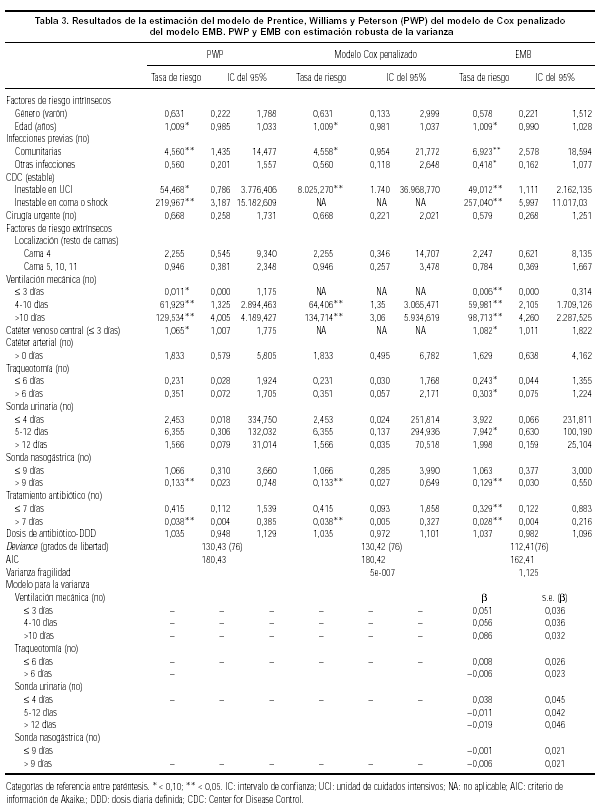
En relación con los resultados del modelo PWP con estimación robusta de la varianza (tabla 3), con una importante excepción, presencia de catéter venoso central durante más de tres días (1,065; IC del 95%, 1,007-1,775), el signo de los estimadores de los parámetros coincide en los tres modelos vistos (modelo AG estándar, modelo AG robusto y modelo PWP), y no ocurre lo mismo con la magnitud ni con la significación de los parámetros. Nótese ahora que variables como la edad (1,009; IC del 95%, 0,985-1,033), la existencia previa de infecciones comunitarias (4,56; IC del 95%, 1,435-14,477), estar inestable en UCI (54,47; IC del 95%, 0,786-3.776,406), estar inestable en coma o shock (219,97, IC del 95%, 3,187-15.182,609), la presencia de ventilación mecánica de cuatro a 10 días (61,93, IC del 95%, 1,325-2.894,463), la presencia de ventilación mecánica durante más de 10 días (129,53; IC del 95%, 4,005-4.189,427) y la presencia de catéter venoso central durante más de tres días (1,07; IC del 95%, 1,007-1,775) aumentan el riesgo de padecer un episodio de infección nosocomial. Contrariamente, la presencia de sondas nasogástricas durante más de 9 días (0,13; IC del 95%, 0,023-0,748) y el tratamiento antibiótico durante más de 7 días (0,04; IC del 95%, 0,004-0,385) lo reducen. Variables tales como género y traqueotomía pierden en este modelo su significación. Resumiendo, no sólo los factores de riesgo intrínsecos (como la gravedad de la enfermedad), sino también los extrínsecos (procedimientos terapéuticos agresivos utilizados en la UCI) llevaron a un mayor riesgo de infección nosocomial durante la estancia del paciente en la UCI.
Los resultados del modelo AG de fragilidad gamma estimado mediante el algoritmo EMB, así como los del modelo de Cox penalizado, también se encuentran en la tabla 3. En el modelo AG de fragilidad gamma estimado mediante el algoritmo EMB, observamos que variables tales como la edad (1,009; IC del 95%, 0,990-1,028), existencia previa de infecciones comunitarias (6,923; IC del 95%, 2,578-18,594), estar inestable en UCI (49,012; IC del 95%, 1,111-2.162,135), estar inestable en coma o shock (257,040; IC del 95%, 5,997-11.017,03), la presencia de ventilación mecánica en todas sus categorías y la presencia de catéter venoso central durante más de tres días (1,082; IC del 95%, 1,011-1,822) continúan aumentando el riesgo de padecer infección nosocomial de forma estadísticamente significativa. Por el contrario, la presencia de sonda nasogástrica durante más de 9 días (0,129; IC del 95%, 0,03-0,55) y el tratamiento antibiótico en todas sus categorías lo reducen, también de forma estadísticamente significativa. Por otra parte, se observa que variables que no eran significativas en el modelo PWP, como la existencia previa de otras infecciones, traqueotomía y presencia de sonda urinaria de 5 a 12 días, pasan a serlo ahora. Estos resultados cambian un poco al observar el modelo de Cox penalizado. Mientras que variables tales como la edad (1,009; IC del 90%: 0,981-1,037), infecciones previas comunitarias (4,558; IC del 90%, 0,954-21,772), estar inestable en UCI (8.025,27; IC del 95%, 1.740-36.968,77), presencia de ventilación mecánica de cuatro a 10 días (64,406; IC del 95%, 1,35-3.065,471), presencia de ventilación mecánica durante más de 10 días (134,714; IC del 95%, 3,06-5.934,619), presencia de sonda nasogástrica durante más de 9 días (0,133; IC del 95%, 0,027-0,649) y tratamiento antibiótico durante más de 7 días (0,038; IC del 95%, 0,005-0,327) continúan manteniendo su significación, otras como traqueotomía, existencia de otras infecciones previas, presencia de sonda urinaria de 5 a 12 días y tratamiento antibiótico durante 7 días o menos la pierden. Por otra parte, el modelo de Cox penalizado parece que es incapaz de estimar los parámetros en algunas de las variables explicativas presentes en el modelo (inestable en coma o shock, ventilación mecánica inferior o igual a tres días y catéter venoso central), lo cual no ocurre en el modelo EMB. Asimismo, el modelo EMB es el que proporciona intervalos de confianza para los estimadores de los parámetros más reducidos.
Adicionalmente, y a diferencia de los demás modelos, el modelo EMB permite observar los factores explicativos de la fragilidad. Como se ve, la varianza de la fragilidad depende únicamente de factores extrínsecos tales como ventilación mecánica, traqueotomía, sonda urinaria y sonda nasogástrica.
Discusión
Como ya se ha dicho, la problemática planteada por la existencia de datos de supervivencia multivariantes hace necesaria la generalización del modelo de Cox de riesgos proporcionales, concretándose ésta en el modelo AG. Este modelo permite trabajar con datos multivariantes; sin embargo, no contempla la posibilidad que las observaciones pertenecientes a un mismo individuo estén correlacionadas, ni la presencia de heterogeneidad individual. Con el propósito de solucionar esto, citamos los principales modelos marginales (modelo AG con estimación robusta de la varianza, modelo WLW y modelo PWP) y condicionales (modelo autorregresivo o markoviano, modelos de fragilidad y modelo de Cox penalizado).
Aun cuando los modelos marginales son capaces de corregir los principales efectos de la dependencia entre observaciones (siempre suponiendo que las estimaciones de los parámetros son consistentes), son incapaces de distinguir cómo los sucesos anteriores pueden influir en el riesgo de desarrollar futuros fallos. Esto último es tratado mediante los modelos condicionales.
El método WLW presenta importantes desventajas. Cook y Lawless20 señalan que el modelo WLW es válido únicamente bajo la posiblemente muy restrictiva hipótesis de censura independiente (restrictiva como consecuencia de las recurrencias). La desventaja más importante es que el método WLW supone que en el instante t todos los individuos (observados en t) constituyen el conjunto de riesgo para la correspondiente recurrencia, con independencia del número de recurrencias previas que tuviese el individuo20,21. Esto no representaría ningún problema si se tratase de diferentes sucesos de un tipo totalmente distinto, pero si se trata de recurrencias del mismo suceso podría ocurrir que algún hecho emprendido con el fin de reducir el número de tales recurrencias redujese el número de las mismas a partir de su implementación (lo mismo ocurriría en el caso de harvesting). Como consecuencia aumentaría la correlación entre los estimadores de los parámetros. Otro problema es que las estimaciones de los parámetros serán consistentes siempre y cuando la función de riesgo esté correctamente especificada.
La principal desventaja del modelo PWP radica en la manera de construir los conjuntos a riesgo, ya que lleva a una «pérdida de aleatorización»22, por cuanto los individuos con más riesgo van saliendo del estudio. Esta pérdida será mayor conforme vayamos moviéndonos a estratos superiores (y cuantos más estratos se consideren). En estos casos, la consistencia de las estimaciones depende de la inclusión de todas las variables relevantes. Por otra parte, tanto el modelo AG como el modelo PWP son sensibles a los errores de especificación de la estructura de dependencia entre los tiempos de recurrencia.
Aunque los métodos marginales cumplen (marginalmente) la hipótesis de riesgos proporcionales, suponen explícita (PWP) o implícitamente (WLW) que la función de riesgo basal varía de una recurrencia a otra22. Como consecuencia, son extremadamente sensibles al cumplimiento (en realidad) de la hipótesis de riesgos proporcionales9. Finalmente, y respecto a las aproximaciones condicionales, los métodos marginales no son totalmente eficientes23,24. La ineficiencia aumentará de forma proporcional al número de estratos (recurrencias) e inversamente proporcional al número de observaciones en cada estrato. En analogía a los modelos lineales es razonable suponer que la ineficiencia también aumentará conforme lo haga la correlación entre recurrencias. Es por tanto de esperar que WLW sea menos eficiente que PWP.
Por lo que hace referencia a los modelos condicionales, sólo comentaremos aquí el problema en los modelos de Cox penalizados. Como argumentábamos anteriormente, la variabilidad que pretenden capturar estos modelos recoge, en realidad, dos fenómenos diferentes, fragilidad y correlación serial. Por otra parte, presentan el inconveniente de que el parámetro de suavizado debe escogerse utilizando técnicas no del todo validadas en el campo de supervivencia.
Situándonos en nuestro ejemplo práctico, de entre los tres modelos marginales presentados en el artículo, el modelo PWP es posiblemente el mejor debido al tipo de datos de que disponemos. El hecho de que, tras experimentar una primera infección, aumente el riesgo de aparición de nuevas infecciones hace que el modelo PWP con estimación robusta de la varianza sea especialmente apropiado, ya que sería posible estratificar los datos para cada episodio de infección.
Por lo que respecta a las estimaciones de los modelos condicionales mencionados en el artículo, el algoritmo EMB de estimación de un modelo AG de fragilidad gamma es el que presenta mejores resultados. Por un lado, es el más eficiente al presentar intervalos de confianza más reducidos, debido quizá a que el algoritmo EMB es capaz de capturar no sólo la heterogeneidad individual, sino también la dependencia serial. Por otro lado, de entre todos lo modelos estudiados, es el que proporciona un mejor ajuste en términos del criterio de Akaike. Finalmente, es el único que permite estimar los efectos explicativos de la fragilidad.
Agradecimientos
Agradezco al Dr. Marc Saez su gran ayuda en la elaboración de este trabajo. Agradezco, asimismo, al Dr. Santiago Pérez Hoyos y a dos evaluadores anónimos sus sugerencias. Este trabajo fue parcialmente financiado por el proyecto 07/50/1998 de la Agència d'Avaluació de Tecnologia Mèdica (AATM) del Servei Català de la Salut, Generalitat de Catalunya.